Maтематика је лијепа као умјетност
Скенирање мозга показало је да сложени низови бројева и слова у математичким формулама могу деловати лепо колико и уметничка дела и музика врхунских композитора. Математичарима су приказане “ружне” и “лепе” једначине, док су били под скенером. Исти емоционални центри у мозгу који реагују на уметност, активирани су и гледањем “лепих” једначина, па истраживачи сугеришу да […]
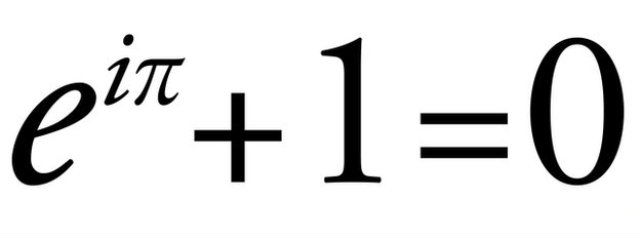
Скенирање мозга показало је да сложени низови бројева и слова у математичким формулама могу деловати лепо колико и уметничка дела и музика врхунских композитора.
Математичарима су приказане “ружне” и “лепе” једначине, док су били под скенером.
Исти емоционални центри у мозгу који реагују на уметност, активирани су и гледањем “лепих” једначина, па истраживачи сугеришу да можда постоји неуробиолошка основа за лепо.
Ојлеров идентитет, или неке од формула Питагорине теореме ретко се помињу у истом контексту са најбољим композицијама Моцарта, или сликама Ван Гога.
Међутим, за потребе студије објављене у журналу Фронтирс ин хјуман неуросајенс 15 математичара имало је задатак да оцени “лепоту” 60 формула.
Један од истраживача, професор Семир Зеки рекао је: “Велики број подручја у мозгу активира се погледом на једначине, али кад неко гледа у формулу која изгледа лепо, то активира област задужену за емоције.
Већина испитаника Ојлерову формулу сматрала је најлепшом.
Она је прелепа и професору Дејвиду Персију са Института за математику и њену примену.
“Она је права класика и нећете наћи ни једну бољу. Она садржи пет најважнијих математичких константи – нулу, јединицу, “е” и “пи”, као и “и”. Обухвата и три најважније математичке операције – сабирање, множење и степеновање”, каже он.
“Будући да су ‘е’, ‘пи’ и ‘и’ врло сложени и наизглед неповезани бројеви, невероватно је да су на једном месту у овој формули. Прво не разумете последице њеног постепеног деловања, можда баш као и кад слушате неки музички комад, а онда вас задиви њен пуни потенцијал”.
Он каже да је лепота извор “инспирације и да даје вољу за нова сазнања”.
Математичар Маркус ду Сотој каже да “апсолутно” види лепоту у математици и да то “мотивише сваког математичара”.
Он каже да воли “мале ствари које је чинио математичар Пјер де Фермат”.
Он је показао да сваки прост број који подељен са четири даје остатак 1, такође је једнак збиру два квадрирана броја.
Тако прост број 41 може бити подељен са четири, а да се добије остатак један, а једнак је збиру 25 (пет на квадрат) и 16 (четири на квадрат).
“Зато ако има остатак један, увек може бити написан као два квадрирана броја. Има у томе нечег лепог. Не очекујете да би две ствари (прости и квадрирани бројеви) могли да имају било шта заједничко, али због доказа увиђате да се међусобно прожимају као у неком музичком комаду”.
Он каже да је сам поступак, а не коначни резултат узбудљив, баш као што “у музичком комаду није довољно да одсвирате последњи тон”.
Испитаници су оценили бесконачне низове Сринивасе Рамануџана и Риманову функционалну једначину као најружније формуле.



